経済成長や景気循環の変動をわかりやすく解説

景気循環の変動の原因は経済学者の見方で大きく変わってきます。経済成長する数式や割出し方を解説します

経済成長や景気循環の変動をわかりやすく解説

[box class=”green_box” title=”記事の内容”]景気循環の解説

古典的景気循環論
サミュエルソンの景気循環論
ヒックスの景気循環論
マネタリストの景気循環論
リアルビジネスサイクル論
シュンペーターの景気循環論の各自の見方

成長会計、コブ＝ダグラス型マクロ生産関数の数式、GDPの割り出し方、成長会計の問題点

これらを解説します[/box]

景気循環とは

景気循環とは、景気が良い時は山、景気が悪い時は谷、といったように波のようなうねりの事を言います

山から山、谷から谷の間の事をサイクルと言います

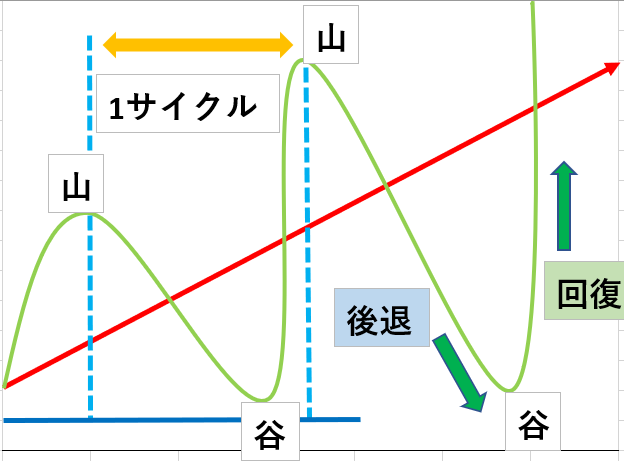
気を付けることは経済成長とは違うことです

経済成長というのは、長期的な流れの景気の事です。短期で景気の良し悪しを言うのではなく、GDP成長率の長期的な変動です

古典的景気循環

過去の景気循環を、おそらくこんな理由じゃないの、と区間を区切って説明していることを、古典的景気循環といいます

古典的なので現代のような理論として考えられていません。かるく見る程度でいいですｗ

前座はこれぐらいにして、有名な経済学者たちが景気循環の変動を説明しているので解説していきます

ケインズ派サミュエルソンの景気循環の見方

結論を先に言うと、計算式によって、経済の中に景気循環という不安定要素があることを説明した人です

ぶっちゃけこれだけわかっていれば十分なのですが、数式も説明しておきます

今年の消費（Ct）とします。去年の所得（Yt-1）とし、今年の消費は去年の所得によって変わると仮定するので
Ct=αYt-1となります

今年の投資を（It）、今年の消費を（Ct）、去年の消費（Ct-1）とすると
今年の投資というのは、今年の消費と去年の消費との差を出します。つまり、消費が多ければ、それだけ生産しなければいけないので、企業の投資は増えると仮定するので
It=β（Ct-Ct-1）となります

今年の国民所得は今年の需要(YD=C+I+G)と等しくなるように国民所得が決まるので、 Yt=Ct+It+Gtとなります

今までの数式をまとめると
Yt-α(1+β)Yt-1+αβYt-2=Gt
となり、この式から差分方程式を作ると、循環の波を数学的に説明できるのです

では数学的に説明してください、と言われても恐ろしい数学的計算になるので、このままそっとしておきましょう。式もおぼえなくていですよｗ

ケインズ派ヒックスの景気循環の見方

ヒックスもサミュエルソンと同様に、差分方程式を作り、景気変動の波を説明したのですが、変動には制限があると考えました

景気の山には限界があって天井のように制限がある。つまり完全雇用によって頭打ちになるはずと考えました

逆に景気の谷も床のように、国民所得の落ち込みにも限度はあると論じたのがヒックスです

まとめると、山や谷の間は上下の区画で制限されているということです

マネタリストの景気循環の見方

マネタリストのフリードマンは、価格は変動するものであり、情報も完全には持ち合わせてはいないと考えます

国民の給料が2倍になると、嬉しくなってその時は使うので、景気は良くなります

人々は情報を完全に持ち合わせていない、と仮定しているので物価も他の価格も2倍になっていることに気付くと

『なんだ、何も変わってないじゃん』となり、お金を使うことをやめてしまいます。これが景気の落ち込みになると論じています

裁量的な金融政策は、短期的にはGDPを持ち上げるけど、長期的にみると元に戻ってしまう

金融政策は裁量的にやるものじゃない、経済規模に合わせて貨幣供給量を出していけばいい、 つまり余計な金融政策が景気変動を起こしているんだ、と言ってるのです

国民所得の成長に合わせて、貨幣供給量を調整することをK%ルールといいます

中央銀行総裁がこんなこと聞いたらショックですね。良かれと思ってやっていることが、逆に景気変動をおこしていた、なんて

リアルビジネスサイクル論

実物的景気循環論と言われています。貨幣や金融は実物経済に影響を与えないとし、経済は常に均衡していると考えます

均衡しているなら景気循環なんて起きないじゃん、となるのですが、この理論は景気が均衡しているところに、技術革新のような外部からの刺激によって変動すると考えます

リアルビジネスサイクル論の斬新なところは、外部からの刺激があるから変動している景気を均衡に持っていく

つまり景気変動を吸収するプロセスを持っているから均衡になるんだってことになり、景気変動そのものが悪いのではなく、変動があるからこそ均衡になるので逆にいい方向に考えよう

これがリアルビジネスサイクル論の一般的な理論の逆転の発想です

シュンペーターの景気循環の見方

シュンペーターの理論は、色々な技術革新が需要や投資の拡大によって景気の波が起きると言っています

例えば、iPhoneや有機EL、５Gのような技術革新が、新市場を作り出し、儲かると考えた投資家は投資を拡大し、工場が増え、雇用が増えるから消費も供給も増え景気が良くなる

ですが、市場があまり盛り上がらなかったとなれば、投資は縮小となり重要や消費も落ち込むので景気が落ち込む

技術革新によって景気変動を起こす考えかたは、リアルビジネスサイクル論に似ています

成長会計

成長会計というのは、経済成長の要因を分析することです

経済成長とはGDP国内総生産のことです

GDPに関する詳しい記事はこちらです

[kanren postid=”6000″]

何の原因や要因があって経済成長していくのかってことを数式を使って分析していきます

もう一度言っておきますが、景気循環とは違います。景気循環とは短期的な景気の波です

経済成長とは、長期的に見たGDPの成長の事です。一国経済の成長を数字にするためには数式を使う必要があります

資本や労働力、それ以外の影響でGDPが成長する生産要素の計算式をコブ＝ダグラス型マクロ生産関数といいます

この計算式を考えた人が、コブさんとダグラスさんが考えた数式なので、このように呼ばれています

コブ＝ダグラス型生産関数

数式はY=AKαL¹-αです

Yは国民所得をいいます。国民所得を計算するために、この計算式を当てはめます

Y＝GDP、Aは定数、Kは資本量、Lは労働量力、αは1未満の正の定数のことです

Aというのは、資本量や労働量以外の要因と考えます

資本と労働の数字が同じであっても、Aが違えば、Yの数字は変わります。労働と資本以外の要素がAになります

例えば技術力だったり、AIの分析だったり、国内のブランド力や信用力によって購買が増えた、などです。目に見えない力と言えばわかりやすいかも

このように資本と労働以外の要因で、Yが変化する要素を全要素生産性といいます

Aは全要素生産性ともいえます

資本量は企業や政府が保有する設備（資本ストック）の量のことであり、労働量は就業数や就業時間で表されます

単純に、GDPは労働力と資本力と全要素生産性と決まる、とだけ覚えておけばOKです

この時点でしびれちゃうでしょ、これも数式は覚えなくていいです。頭わいちゃいますからｗ

成長会計は便利

Y=AKαL¹-α の対数を取って、時間で微分して、それから……この時点で頭真っ白になりそうです

Y=AKαL¹-α という数式を使えば、簡単に経済成長を表すことが出来ます

日本の場合、αは0.5と言われているので、各省庁の方や内閣府で働く統計数字を出す人達は、この数式を使って経済成長の数字を出しています

これまで数式を紹介しましたが、当てはめて計算するには統計的な数字のデーターが必要です

各省庁の統計データーがあれば、できるのではないかと思うのですが計算したことはありません

なぜならデーターが無いからです

ここでは、こういう計算の数式がありますよと紹介しました

知識として覚えておいてもらえればいいと思っています

成長会計の問題点

日本の経済成長をコブ＝ダグラス型マクロ生産関数の数式を使って数字を出していますが、実は確実な数字ではないのです

なんで使ってるかというと、わかりやすくて計算しやすいからです

日本の経済から割出せる数字を、そのまま数式に当てはめることが出来るからです

問題点というのは、他の国で考えると、使えない国も存在していて世界共通で使える数式ではないのです

複雑な数式を使った別のマクロ関数もあるのですが、上手く割出せず、現実経済を分析できないのです

このまま使い続けていいのか？っていう議論もあるのですが、では他の方法があるのかと言われれば無いので、しかたなく使っているだけなのです

まとめ

景気循環と経済成長は違います

経済学者によって循環の見方は変わってきます

成長会計は経済成長を分析するツールの事

GDPは労働力と資本力と全要素生産性できまる

コブ＝ダグラス型マクロ生産関数の数式は覚えなくてよい