2つのマクロ消費関数の違いを3大仮説を使って矛盾なく説明します

マクロ消費関数とは、所得と消費の関係をグラフで表したものです。経済の変化を2つのグラフにあてはめても説明のつかない事が多々あり、変化の動向を説明したのが3大仮説です。消費関数と仮説の関係を解説します。

2つの消費関数と3つの仮説の違いを考えていませんか？

消費関数グラフの違いを理解すれば、3つの仮説の違いも同時に理解できます。

というのも、消費関数の違いを3つの仮説で説明しているからです。

ここでは、2つの消費関数の違いや基礎、3つの仮説をグラフを使って解説します。

この記事からわかることは、消費関数グラフの計算や基礎、3つの仮説を理解できます。ライフサイクルの計算を使って年収から年間の消費金額を割出すことができるので、自分でライフプランを作成できます。

ポイントは3つです。

では具体的に解説していきます。

2つの消費関数

マクロ経済学には現実経済の消費や所得を数式に当てはめて計算することを消費関数といいます。かつて2つの数式に違いがあり論争となりました。

この2つの数式を説明します。

ケインズ経済学に関する記事はこちらです。

[kanren postid=”5978″]

特にケインズ型の計算は基礎となるので具体的に解説します。

ケインズ型消費関数とは

消費関数とは、何かと何かの数の関係です。

マクロ経済学でのケインズは、消費量というのは所得に大きく関係するんじゃないか、と定義しています。

つまりお金をたくさん稼ぐ人は消費もそれなりに増える、と考えます。

このような考え方を一国経済に当てはめて考えると、国民総所得が増えれば消費量も増えるでしょ、という定義のうえ消費関数を解説します。

ケインズ型の計算式

消費関数の式として消費量Cと国民所得（GDP：Y）との間に関係があると考えました

C＝a＋bYがケインズ型消費関数となります。

基礎消費＝a（a＞0）
限界消費性向＝b （0＜b＜1）

この２つを具体的に説明します。

基礎消費

基礎消費を別名、独立消費とも言いますが基礎消費とします。

基礎消費とは、最低限の生活をするための消費です。例えば、生活するために必要な所得を全て消費すると考えます。

生きるためだけに消費するので他のことに消費をしない。このため所得は残らない。

つまり所得はゼロ、消費だけの関係になります。（a＞0）のaは基礎消費なので0より高くなる。

限界消費性向

経済学の限界とは1単位の事を言います。

消費関数で言えば1所得をえた時、どれぐらい消費が伸びるかを表した数字です。

（0＜b＜1）の0とは、基礎消費と同じで所得分は全て消費すると考えるので所得と消費は0となります。

1は、稼いだ所得を使わず全て貯金に回すので、消費せず保持するとなり稼いだ所得は1のままとなる。

bは、稼いだ所得は〇消費して〇貯金すると考えるので中間となります。消費と貯金の割合は何でもいいです。

ケインズ型の場合、7割消費すると考えるので0.7となります。なぜ7割なの？と聞かれてもそれが定数とされているので7割です、意味はありません。

a,bは定数です。定数とは矛盾せず変化せず決まっている数字です。
aが1増えると、bが0.7増えます。

そのためケインズ型消費関数はC＝1+0.７Yとなります。

消費関数の数式をグラフ化

Yが100の時 C＝100+0.7×100＝170がB点
Yが200の時 C＝100+0.7×200＝240がC点
Yが300の時 C＝300+0.7×300＝310がD点 となります

この消費関数の式では一直線になります。なぜなら70づつ増えているからです。

最初A点の100上がる理由としては、基礎消費で説明した通り稼いだ所得は全て消費するので、所得は0となりますが、消費だけはしているので消費分、上にあがります。

単純に100消費したので100上がり、次から所得が100増えると消費が70増えるといった感じです。

[box class=”red_box” title=”これだけ覚えておこう”]ケインズ型の消費関数は横に1の時は、縦に0.7上がる。[/box]

このケインズ型消費関数に、それ本当なのか、と異論を唱えた人がクズネッツです。

クズネッツ型消費関数とは

クズネッツ型消費関数は、ケインズ型消費関数が正しいかどうかを検証するために、米国の消費と所得の関係データー（1869～1943年）を調べました。

この調査から次の事が明らかになってきました。

驚いたことにケインズ型の消費関数にならなかったのです。数式は異なるものでした。

aとbが0.9に変化しシンプルな数式となりC=0.9Yとなります。

あんまり変わらんじゃないか、と言われればそうなのですがクズネッツ型はある特徴がありました。

それは長期の視点だと当てはまるのです。

C＝0.9Y クズネッツ型長期消費関数
C=a+bY ケインズ型短期消費関数

と定義したのです。

短期と長期の消費関数グラフ

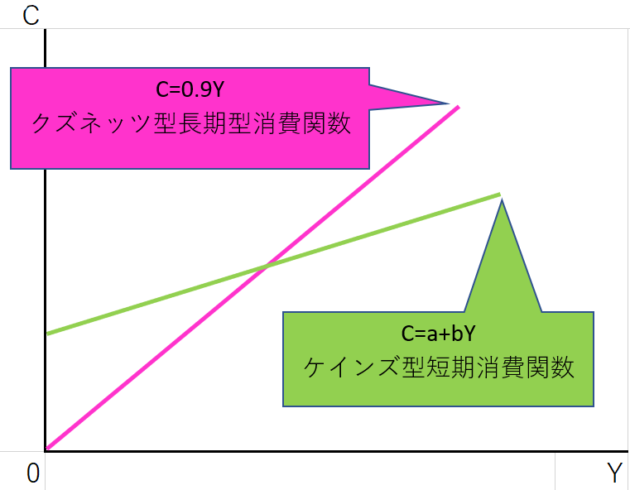
クズネッツ型消費関数は、Yが0の時は消費0になるのでスタートは0となります。

ケインズのように消費だけとは考えず、所得が増えれば消費も増えると考えるので斜めになり45度に近い角度になります。

では長期と短期では消費関数が異なるのか？と論点について論争が巻き起こりました。

それがマクロ消費論争です。

ケインズ型消費関数とクズネッツ型消費関数の計算やグラフの解説は以上です。ここからは、このグラフを使って3大仮説を解説します。

マクロ消費論争3大仮説

マクロ消費論争とは現実経済を2つの消費関数に当てはめた時に、矛盾なく説明できる仮説のことをいい、特にこの3つが一番説得力があると言われています。

というのも、ケインズ型消費関数を元に経済をあてはめても、説明できない不可式な事も多く消費関数に当てはまらないことも多々あったからです。

これら3つの理論を使って消費関数を説明していきます。

相対所得仮説

ケインズ型短期消費関数の考え方は、今稼いでいる所得によってのみ決まると定義しています。現在の所得なので絶対所得とも言います。

ですがデューゼンベリーは、そうではなく現在の所得に加えて、過去の所得や相手の消費も影響受ける、と考えた理論が相対所得仮説です。

相対所得仮説には、歯止め効果とデモンストレーション効果の2つあり、短期と長期の消費関数を説明します。

歯止め効果

贅沢していた人が急に明日から質素な暮らしに変更できるかと言えば、おそらく無理です。絶対ではないですが 人の消費は習慣になっているからです。

つまり過去からの習慣は急には変えられません。このように習慣化された消費を歯止め効果といい短期の消費型です。

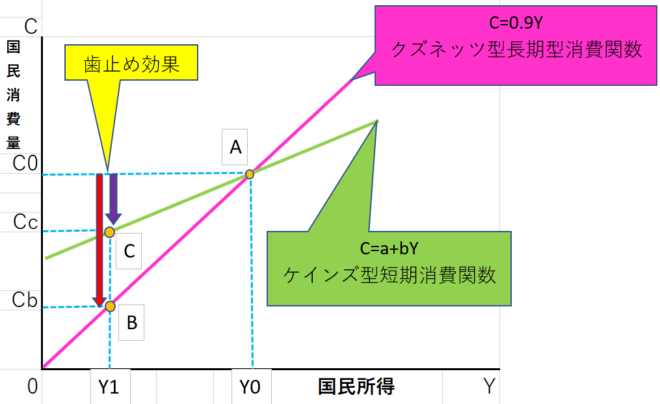
A点が今の状態とし仮に所得がY0からY1に減ったとします。

長期視点で見るとB点まで減少し、短期視点だと歯止め効果でC点で止まります。

この他では契約もそうです。契約している期間というのは急に変更できないのでしばらくは払い続けます。これは習慣化された消費と同じです。

反対に長期で長い間お金が無くなると質素な生活となり、消費もそれなりに減るので長期視点では歯止め効果が無くなりB点まで下がります。

デモンストレーション効果

これは歯止め効果と似ています。デモンストレーション効果というのは、相手の消費が自分に与える影響を表したものです。

仮にY0からY1に自分の所得が減ったとします。でも相手の所得が減ったかどうかはわかりません。

人の見栄とは相手からどう見られたいか気になるので、いつものように消費します。自分の所得が減ったからといって急に質素な暮らしをするのも嫌だな～という感じです。

つまり相手の消費に合わせて、こちらも消費する感覚です。これが短期視点となるのでC点となります。

長期視点では、皆の所得が減ったと分かれば減ったのは自分だけじゃない、と安心して消費を減らすとのでB点まで下がります。

ハッキリ言って強引な屁理屈にもみえますが、2つの仮説はこんな感じで覚えてください。

以上の2つが相対所得仮説の説明です。

恒常所得仮説

消費量は現在の所得ではなく長期平均所得で決まる、とフリードマンが考えた仮説が恒常所得仮説です。

長期的に所得が減れば消費も減り、逆に所得が増えれば消費も増えます。

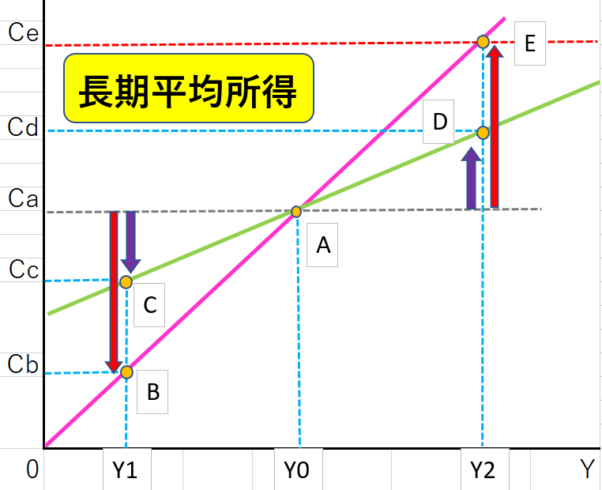
恒常所得仮説は長期視点での考え方です。短期で所得が減れば消費もわずかとなりC点となります。

長期で所得が減ると消費も大きく減るのでB点となるのです。

ですが逆に所得がY0からY2になると所得が増えるので、A点の起点よりも短期だとD点、長期だとE点まで消費が増えるということになります。

ライフサイクル仮説

人は最も合理的に考えて行動する、を説明できる有力な仮説とされています。

なぜなら若いうちはある程度使って、老後のために貯金を残しておこう、と考えるからです。

人は一生涯の人生を考えて1年間の消費を決めるので、所得は消費だけじゃなく資産にも影響を受けてしまう、という考えをアンドウ、モジリアーニ、ブランバーグが提唱しました。

これをライフサイクル仮説といいます。

ライフサイクル仮説の消費計算

生まれてから生涯を終えるまでの総所得と資産を足し合わせた合計から、1年間の消費を割出す計算です。

消費は現在の所得Yだけでなく資産Wの影響も受ける、と考えます

この条件をCT＝W＋ｔYにあてはめて計算します。

• 一生涯の消費額＝C×50
• 一生涯で使えるお金＝生涯所得＋資産＝30×500＋1000となります

1と2が等しくなるように計算します。

C×50＝30×500＋1000となります。この計算にはルールがありイコール（＝）より反対位置に移動すると逆になります。

×は÷となり、＋は－となります。これを踏まえC×50の×50を＝より右に移動します。

C＝（30×500＋1000）÷50（移動したので×から÷に変わっている）
C＝16000÷50(かけ算を先にして足すのは後になる)
C＝320万円となります。

このことから1年間の所得500万円から消費できるお金は320万円となります。

簡単なのでやってみてください。

ライフサイクル仮説のグラフ

長期間Y0からY1に減ると資産も大きく減るので消費はB点まで落ち込む。短期間では資産は急に減らないので消費はC点までしか落ち込まない。

[box class=”red_box” title=”ポイント”]短期での資産は一定だが長期では所得に連動し資産も増える[/box]

3大仮説の評価

3大仮説ともに長期の消費関数、短期の消費関数を矛盾なく説明しています。

相対所得仮説は、過去の消費と他人に合わせた消費。
恒常所得仮説は、長期平均所得に合わせた消費。
ライフサイクル仮説は、資産という概念を導入した消費。

図を見てわかったと思いますが、全て似たようなグラフです。

短期と長期の理由を無理やりこじつけのように論じて納得させているだけで、絶対的な根拠がありません。

確かにその仮説なら、なんとなく納得いく、この程度なのです。

一応マクロ経済学としての消費関数は3大仮説が確立しているので説明しましたが、僕的な見方はかなり微妙な仮説です。

なぜなら現実経済は複雑であり、3つの仮設にあてはまらない現象が数多く存在しているからです。

まとめ

消費関数は2つあり、ケインズ型消費関数は短期、クズネッツ型消費関数は長期です。

短期と長期では消費関数のグラフは異なる。

3大仮説には、相対所得仮説、恒常所得仮説、ライフサイクル仮説がある。

ライフサイクル仮説の関数を通して、ケインズ型消費関数とクズネッツ型消費関数を説明できる。